天体测量法
交叉匹配法
找到一个图像中源像素坐标与另外一个天球坐标参考目录(或另一个观测图像的源像素坐标)的最佳几何匹配关系。标记参考列表为 $R$ ,图像列表为 $I$ ,两者之间的转换关系为 $F_{R \rightarrow I}$ 。为了找到匹配的点源对,需要知道转换函数,反之亦然,为了推导出转换函数,需要知道匹配点。
在天文应用中一个更普遍的假设是$F{R\rightarrow I}$是一个相似变换,比如旋转、放大等,$F{R\rightarrow I} = \lambda A r + b$,矩阵 A 是正交矩阵的 $\lambda$倍,b 是平移转换,r 是点的空间矢量矩阵,在大视场中,会存在高阶失真项,有时候图像会包含大量的源,图像匹配更难。为此,本文提供一种更普遍的算法来实现大视场高阶项失真改正的天体测量方法,该算法在大视场图像中表现的更快更加稳健,而且需要的假设更少。
>
- 与线性项相比,失真是不可忽视的但较小
- 在参考点和图像点之间存在平滑的转换
- 点列表有相当多的共同来源
- 转换是局部可逆的
对称点匹配
首先假设 $F{R \rightarrow I}$ 已知,找到 $R$ 和 $I$ 之间的匹配点,应该首先将参考点转换到图像的参考框架中 $R’ = F{R \rightarrow I}(R)$, 然后就可以执行 $ R’$ 和 $I$ 的点匹配;$R’$中的一点在 $I$ 存在一个很接近的一点,就认为是一对匹配点。
>
假设一维参考列表中有按升序排列的 N 个点(开始时使用快速排序法执行一次即可),时间尺度为 $O(N log N)$
关于二维点的列表,我们再次假设这些点是由它们的 x 坐标[初始排序 $O(N log N)$]以升序给出的,并且它们被均匀地分布在单位面积内。在 x 方向排序时间与一维一致,但两点间的欧几里得距离不一定最小,除了两点间距离的期望值是 $1/ \sqrt N$ 外,还需要在具有相同宽度和高度的条带内比较点,其时间尺度为 $O(\sqrt N)$,所以匹配两个二维目录的对称点需要的时间尺度为 $O(N^{3/2} log N)$。
找到转换函数
任务是找到 $R$ 和 $I$ 之间的转换关系,该算法的第一步也是最重要的一步是找到基于三角匹配顶点的初始变换函数 $F{R \rightarrow I}^{(1)}$,使用该转换函数,完成对称点的匹配,进一步改善转换函数 $F{R \rightarrow I}^{(i)}$,即使用迭代的方法来改进,从而增加对称匹配点数。
三角匹配
三角匹配法用于初始转换函数,函数 $F_{R \rightarrow I}$ 主导项是线性部分,所以在 $R$ 和 $I$ 之间的一阶近似存在一个放大尺度(除了旋转、比例尺和平移外)
三角空间
- 定义归一化三角空间 $T^{min}$,其坐标对原始列表坐标的变换不明显,即所有的相似三角形可以由相同点表示,与比例尺无关。$$T^{mix}{x} = p/a \tag {1}$$ , $$T^{mix}{y} = q/a \tag {2}$$ a、p、q 是按降序排列的三角形边长。混合空间三角形的坐标是边长的连续函数,但确实方向信息。但对于大量的点和三角形来说,确定指向很可靠。
chrial 空间三角形,$$T^{chir}{x} = b/a \tag {3}$$ $$T^{chir}{y} = c/a \tag {4}$$, a、b、c 为逆时针方向的三个边,a 为最长边。在这个空间中,具有不同指向的相似三角形是有不同的三角形,缺点是不连续。但可以定义既可以连续,又能保证比例尺的参数,首先沿着 $T{x} + T{y} = 1$将三角形翻转,就可以将等边三角形移动到原点,接下来应用整个空间的径向放大率将 $T{x} + T{y} = 1$线沿着 $T{x}^2 + T{y}^2 = 1$弧移动。
continuous 空间三角形最佳三角形的大小由两个因素决定:大三角形的畸变和三角形参数的不确定性,小三角形的大小与顶点的天体测量误差相当
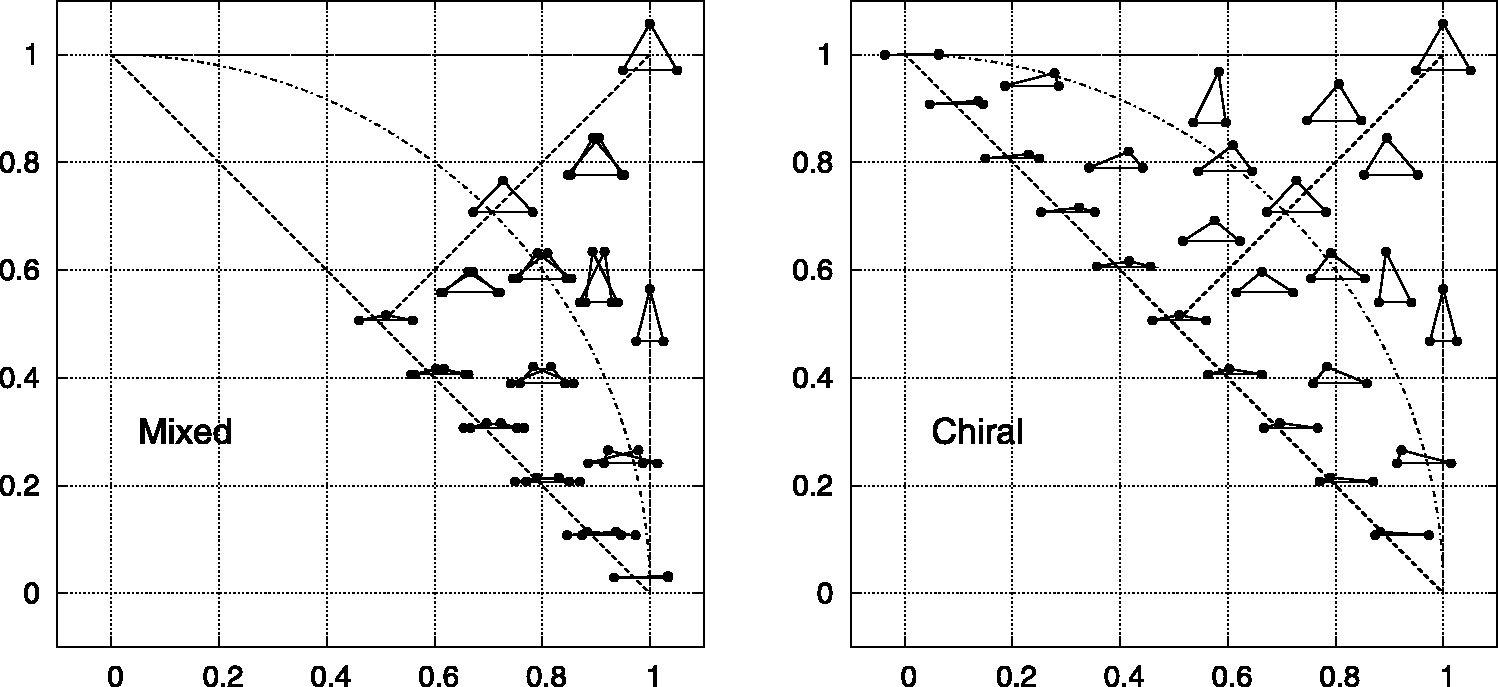
最佳三角形集
N 个点可以形成 $N^3 /6$ 个三角形,在大视场中包含万以上的点,形成完整的三角形列表显然不现实。首先存储和处理这么多的三角形是电脑无法完成的。
第二,完整列表中有很多不适合使用的三角形。比如在 $I$ 中的大三角形在 $R$ 中会有显著的扭曲现象,因此在三角空间中应该用不同的坐标系表示才合理。最佳三角形的大小由两个因素决定:大三角形的畸变和三角形参数的不确定性,小三角形的大小与顶点的天体测量误差相当。估计扭曲因子 $f_d$ 的值,$f_d \simeq |(sin d - tan d)/d| \simeq |1 - cos d | $, 该值为正交投影和日晷投影的差值,$d$ 为视场中心开始测量的径向距离。在 HATNet 中($d = D \simeq 6^{\circ}$ to the corners),畸变效应在三角空间产生的误差为 $fd L/D$ , $L,D$分别为所选三角形的大小和图像的特征大小。最佳三角形的大小估计值为 $L{opt} = \sqrt {\frac{\delta D}{f_d}},\delta 为天体测量的不准确值$,在 HATNet 中 $D = 2048 , fd = 0.005 , \delta = 0.01 , 得到最佳三角形大小为 L{opt} \simeq 60 - 70 pixels $.
第三,处理许多三角形可能会由于大量点导致产生过于饱和的三角形空间,并可能产生意想不到的三角形匹配
扩展德劳内三角形
Delaunay triangulation 是一种在点集内快速而稳健的产生三角网的方法,Delaunay triangulation 是不相交的三角形,其中任何三角形的外接圆都不包含任何其他三角形的点。由欧拉定律可以得到 N 个点形成的德劳内三角形数为 $T_D = 2N -2 -C$ ,其中C是点集的凸包上的边的数量。大量的点数时,近似为 $T D = 2N$ ,选择的距离在 $T{opt}$ 范围内的点集,则可以形成的德劳内三角形为 $2 D^2 / L^2_{opt}$ ,虽然可以实现快速匹配,但不具有稳定性,具体的原因如下
>
其对星表中的一个点的移除非常敏感.根据多面体公式,一个点会有六个邻近点,属于六个三角形,一般会在图像中的最亮星去建立 $I$,但会由于过饱和或落在坏的列中而消失.
其次,更重要的是,不能保证 $R$ 和 $I$ 中点的空间密度是相似的.
德劳内三角形的数量少于所需的三角形数量
因此需要扩展德劳内三角形的数量,定义一个水平线 $\ell$ , 对于任意给定的点 P ,从 N 个点集选择所有可以经过德劳内三角形 $\ell$ 边连通点 P 的点,一个数据点可以扩展的三角形数量为 $$ T_{\ell} = (3\ell^2 + 3\ell + 1)(3\ell ^2 + 3\ell)(3\ell^2 + 3\ell -1 )/6 \tag{5}$$
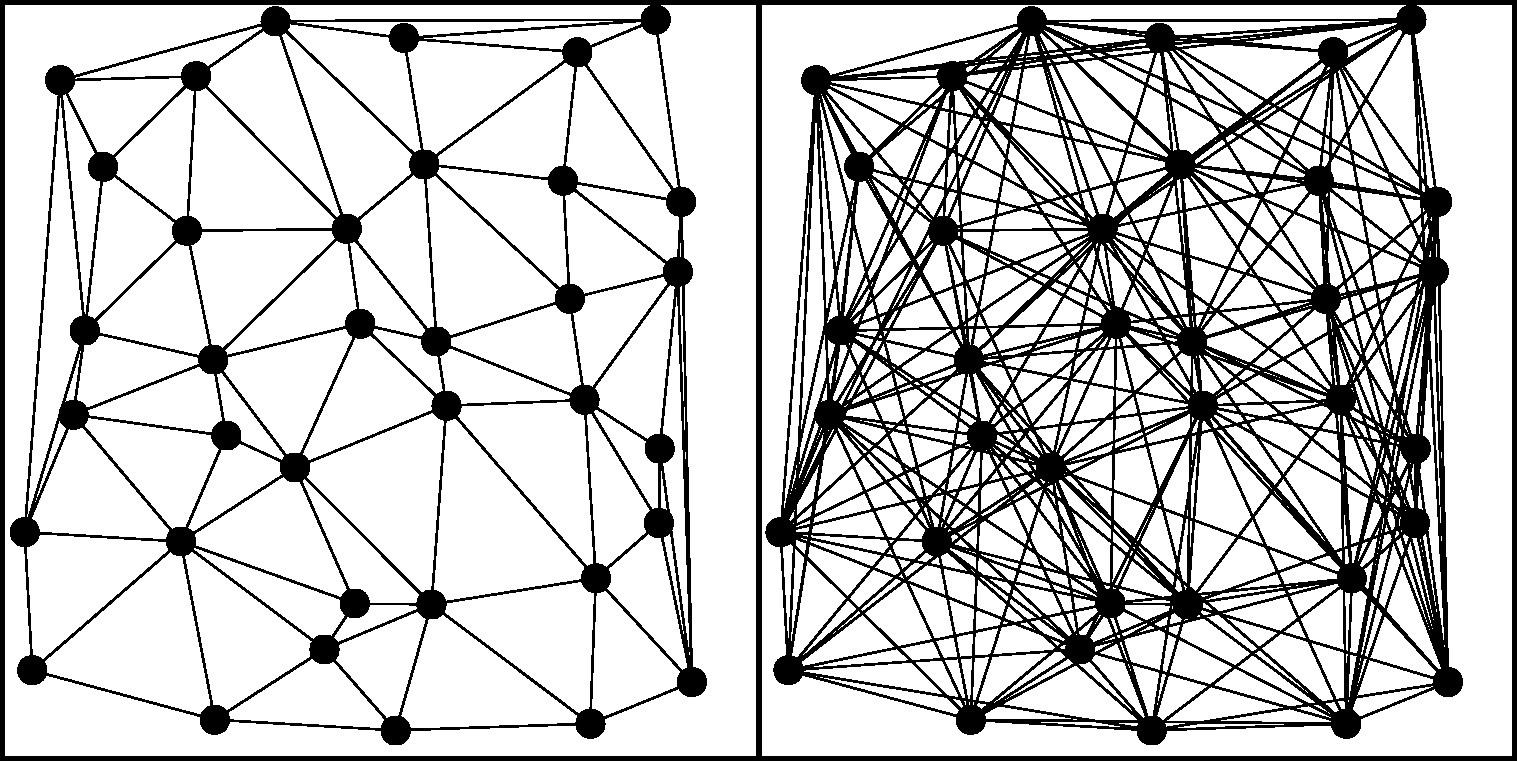
三角形空间实现三角形匹配
如果已知参考目录和输入列表的三角形集合,则可以使用第2节中描述的对称点匹配在标准化的三角形空间(它们由二维点表示)中匹配三角形,接下来我们创造一个 $N_R \times N_I$ 的 vote 矩阵 $V$, $N_R$ 和 $N_I$ 分别为参考目录和输入列表的点数,用于产生三角形。每一个匹配的三角形分别对应参考目录的三个点和输入列表的三个点,即 $r_1,r_2,r_3 and i_1,i_2,i3$ , 增加的三个矩阵元素为 $V{r_1i1},V{r_2i2} , V{r_3i_3}$ ,增加的矩阵元素数量依赖于三角形空间中匹配三角形的距离,距离越近,就有越多的 vote 。建立了 vote 矩阵之后,我们选择矩阵的最大元素,并且引用这些行和列索引的适当的点认定为是匹配的点源,选择最大的40%的矩阵元素即可
转换函数的统一性
如果从三角形匹配中知道可能点对的一个初始集合后,就可以使用多项式拟合来将参考点集转换为输入点,在变换之前,我们的假设是变换中的主导项是相似变换,这意味着它的齐次线性部分几乎应该是一个单位性算子,即 $A^+ A = I$ ,相似变换可以写为 $$r^{‘} = \lambda A r + b \equiv \lambda \begin{pmatrix} a & c \ b & d \end{pmatrix} r + b \tag{6}$$ $\lambda \neq 0,a,b,c,d$ 分别为给定旋转角的正弦和余弦值,即 ($a = d , b = -c$) 。分离转换函数的线性部分,其是旋转和放大的组合矩阵,定义一个 2x2 的酉矩阵 $$ \Lambda^2 \equiv \frac{(a \mp d)^2 + (b + c)^2}{a^2 + b^2 + c^2 + d^2} \tag{7}$$ 加减号代表正反转变换,$\Lambda = 0$ 表示扭曲变换,$\Lambda$ 可以很好的估计初始的转换函数是否足够好,如果转换函数有误差,可以通过迭代直到 $\Lambda$ 达到满意。
点匹配
参考目录 $R$ 和图像 $I$ 中的点匹配处理过程如下
在 $R$ 和 $I$ 上分别产生两个三角形集 $T_R$ 和 $T_I$ ,
- 在第一次迭代时,只生成Delaunay triangles
- 随后,如果需要的话,可以根据水平线 $\ell$ 生成扩展 Delaunay triangles , 增加三角形数
使用对称点匹配法在三角形空间中匹配这两个三角形集
选择一些可能的点对,使用vote 矩阵算法(产生 $N_0$ 对点对)
使用最小二乘法得到初始的平滑转换函数 $F_{R \rightarrow I}^ {(1)}$
- 检查 $F_{R \rightarrow I}^ {(1)}$ 的统一性( unitarity)
- 如果其大于给定的阈值 $O(f_d)$ ,增大给定的 $\ell$ 值,返回到第一步,如果小于,跳转到第五步
使用初始的转化函数将 $R$ 转换到图像的参考框架下,即将参考目录转换为图像列表 $R’ = F_{R \rightarrow I}^{(1)}(R)$
在 $R’$ 和 $R$ 之间执行对称点匹配,产生 $N_1 \gt N_0$ 个点对
基于更多的点对数重新定义转换函数,产生转换函数 $F_{R \rightarrow I}^ {(i)}$ ,$i$ 为迭代的次数
如有必要,重复第5,6和7步,增加匹配点的数量,并精确转换函数
对于大多数天体测量的变换和失真问题,认为在局部可以用相似变换近似解决,关键的一步是最初的三角形匹配,并且由于使用了局部三角形,这证明是一个稳健可靠的的过程,转换函数的平滑处理一般使用多项式拟合法,拟合的阶数取决于失真的程度
软件的实现和应用
软件的实现
坐标匹配和转换算法,程序grmatch实现匹配点集,包括三角空间生成,三角匹配,对称点匹配和多项式拟合,即第三部分的步骤1-4,grtrans使用grmatch输出的变换系数变换坐标列表,也可以实现手动点匹配或外部软件产生的点对的多项式拟合。通过结合这两个程序,可以很容易的得到 FITS 文件的 WCS 信息,也可以对拍摄到的图像进行天体测量和恒星识别,其具体步骤如下:
- 对所有的观测,使用 2MASS 参考目录,参考列表包括源标识码、原始天球坐标、光度和映射坐标
- 输入列表为每个图像产生的星表
- 使用 grmatch 来匹配输入的星列表和参考星列表,是在映射坐标 ($\xi,\eta$) 和 探测到的图像坐标 (X,Y) 之间匹配,输出文件为匹配列表和多项式拟合的参数列表和一些统计数据。
- 参考星列表 ($\xi,\eta$) 使用 gtrans 转换为图像的坐标 (X,Y)
我们注意到这个过程的关键部分是第三步。这可以通过使用许多参数进行微调,其中最重要的是多项式阶数,下图展示了两个向量图,其显示了对于典型的HATNet图像使用二阶和四阶多项式变换的变换的参考坐标和检测到的星形坐标之间的差异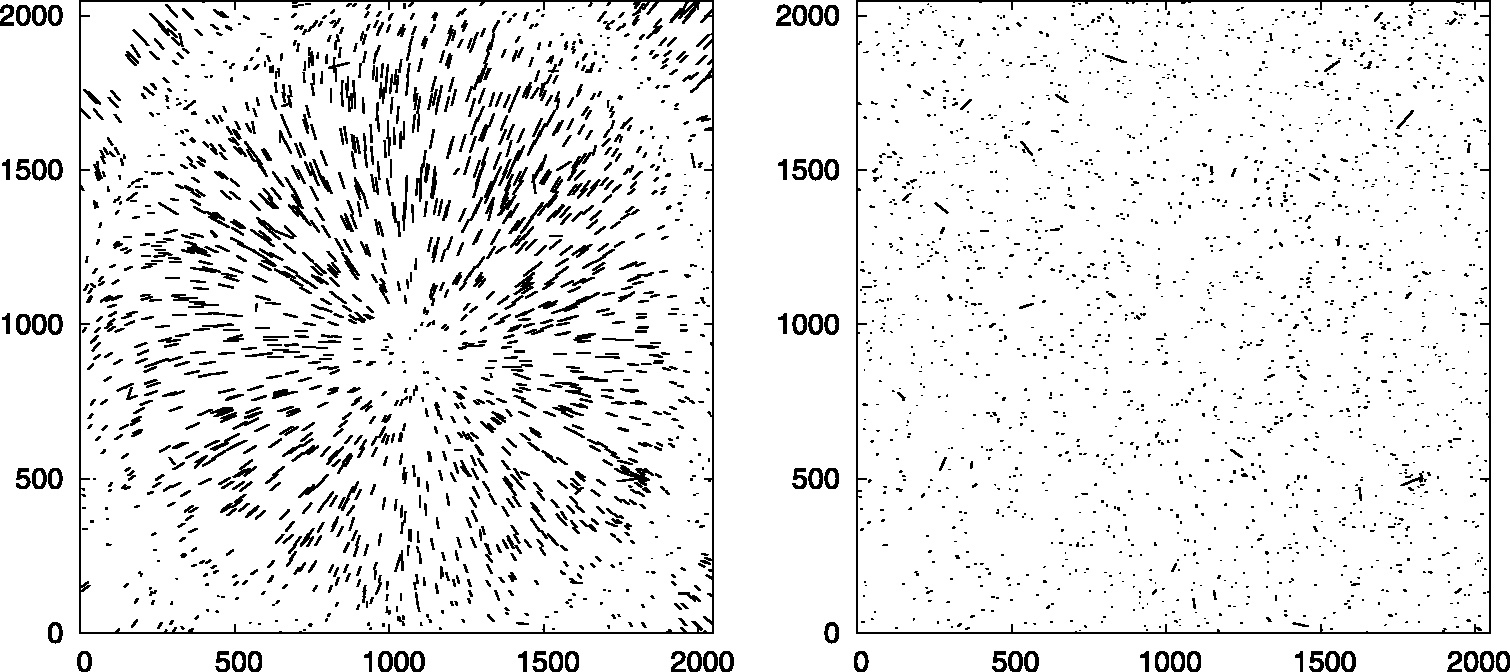
在第一种情况下,通过使用二阶融合,保留了有限的径向结构,并且位于图像角落的恒星由于光学中的大变形而不是均匀匹配的,而使用四阶拟合,图像的所有片段都是匹配的,残差也较小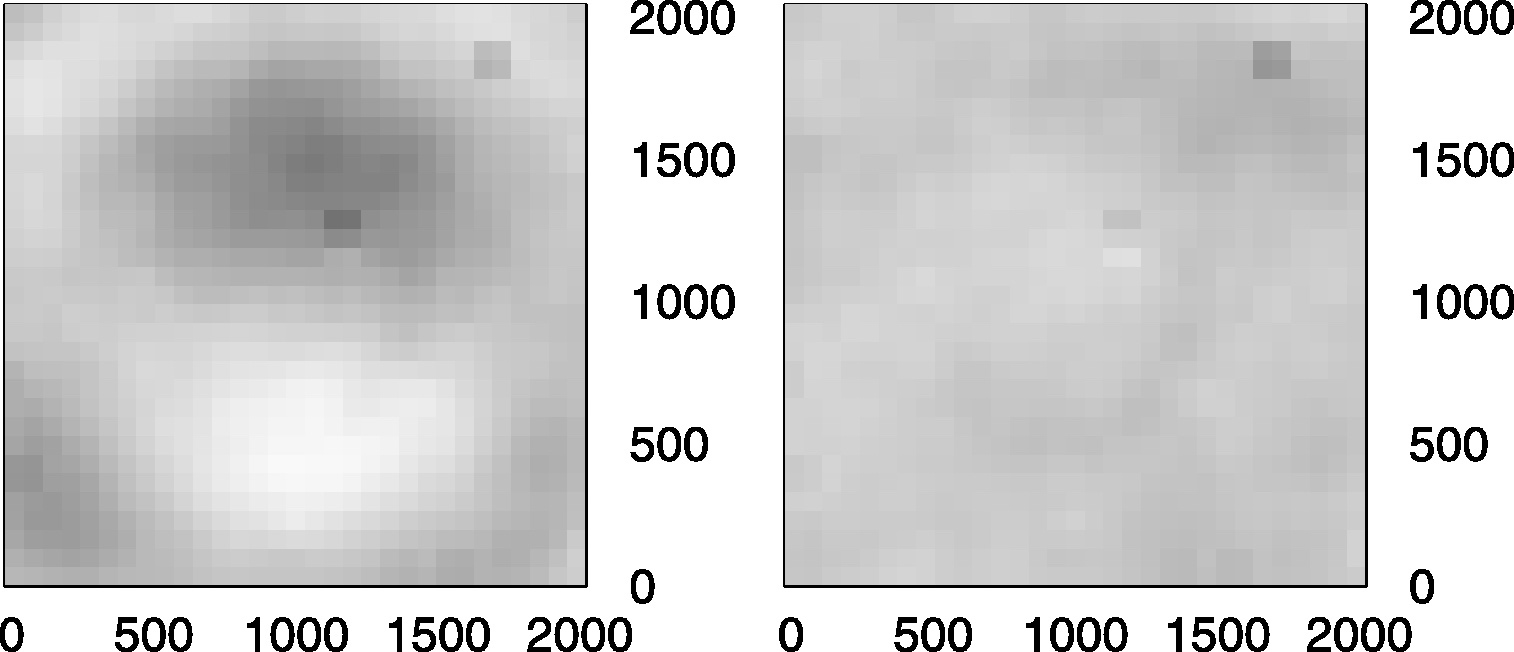
使用四阶(左)和六阶(右)多项式拟合的变换参考的Y坐标与典型HAT场的输入星坐标之间的差异
虽然程序速度很快,但我们注意到这个过程中最耗时的部分是三角测量生成和三角形匹配本身,重点是将参考目录目标转换为输入列表信息,才可以利用对称点生成的三角形完成匹配
结论
我们提出了一个对二维点列表的两个交叉匹配稳健算法。这个任务是双重的:赵大鹏两个列表之间平滑的空间转换,并交叉匹配点,这两个步骤交织在一起并且以迭代的方式执行,直到达到令人满意的变换和匹配率。
- 基于三角形匹配找到点列表之间的初始转换
- 考虑到场的畸变和天体测量误差,我们计算出三角形的最佳尺寸和数量
- 确定了两个列表之间的转换之后,可以检查关于主导项的线性的最初假设是否足够好